Modelos y Sumilación
jueves, 15 de agosto de 2013
martes, 13 de agosto de 2013
Relaciones de términos Blogs Compañeros
Francisco Barragán
http://fcobarragansimulacion.weebly.com/modelo-montecarlo.html
Modelos.- Es una representación o abstracción de una situación u objeto real, que muestra las relaciones (directas o indirectas) y las interrelaciones de la acción y la reacción en términos de causa y efecto.

¿Cuándo se utiliza el método de Monte Carlo ?
Juan Arias
http://ariasnicola.blogspot.com/2013_08_01_archive.html
Francisco Barragán
http://fcobarragansimulacion.weebly.com/modelo-montecarlo.html
Modelos.- Es una representación o abstracción de una situación u objeto real, que muestra las relaciones (directas o indirectas) y las interrelaciones de la acción y la reacción en términos de causa y efecto.

¿Cuándo se utiliza el método de Monte Carlo ?
El uso de los métodos de Monte Carlo como herramienta de investigación, proviene del trabajo realizado en el desarrollo de la bomba atómica durante la Segunda Guerra Mundial en el Laboratorio Nacional de Los Álamos en EE. UU. Este trabajo conllevaba la simulación de problemas probabilísticos de hidrodinámica concernientes a la difusión de neutrones en el material de fisión. Esta difusión posee un comportamiento eminentemente aleatorio. En la actualidad es parte fundamental de los algoritmos de Raytracing para la generación de imágenes 3D.
Juan Arias
http://ariasnicola.blogspot.com/2013_08_01_archive.html
Algoritmo Metropolis Hastings
En las estadísticas y en física estadística , el algoritmo de Metropolis-Hastings es una cadena de Markov Monte Carlo método para la obtención de una secuencia de (MCMC) muestras aleatorias a partir de unadistribución de probabilidad para el que el muestreo directo es difícil. Esta secuencia se puede utilizar para aproximar la distribución (es decir, para generar un histograma), o para calcular una integral (tal como un valor esperado ).
Muestreo de Gibbs
En matemáticas y física, el muestreo de Gibbs es un algoritmo para generar una muestra aleatoria a partir de la distribución de probabilidad conjunta de dos o más variables aleatorias. Se trata de un caso especial del algoritmo de Metropolis-Hastings y, por lo tanto, del MCMC.
Jeferson Llerena
Cadenas de Markov
Una cadena de Markov es un modelo matemático de sistemas estocásticos donde los estados dependen de probabilidades de transición. El estado actual solo depende del estado anterior. El método de Monte Carlo es un método no determinístico o estadístico numérico usado para aproximar expresiones matemáticas complejas y costosas de evaluar con exactitud. Las técnicas de Monte Carlo vía cadenas de Markov permiten generar, de manera iterativa, observaciones de distribuciones multivariadas que difícilmente podrían simularse utilizando métodos directos. La idea básica es muy simple: construir una cadena de Markov que sea fácil de simular y cuya distribución de equilibrio corresponda a la distribución final que nos interesa. Smith y Roberts (1993) presentan una discusión general de este tipo de métodos.
miércoles, 7 de agosto de 2013
lunes, 5 de agosto de 2013
jueves, 1 de agosto de 2013
Método de Monte Carlo
¿Qué es el método Monte Carlo?
Matriz de transmisión:
Partiendo de esta información podemos elaborar la matriz de transición.
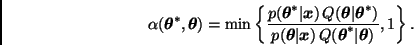
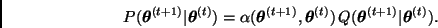
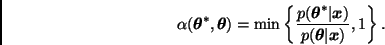
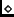 Caminata aleatoria. Sea
Caminata aleatoria. Sea 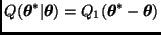 , donde
, donde 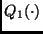 es una densidad de probabilidad simétrica centrada en el origen. Entonces
es una densidad de probabilidad simétrica centrada en el origen. Entonces
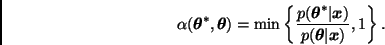
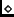 Independencia. Sea
Independencia. Sea 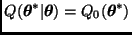 , donde
, donde 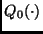 es una densidad de probabilidad sobre
es una densidad de probabilidad sobre  . Entonces
. Entonces
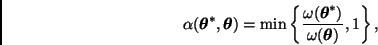
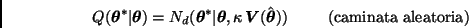
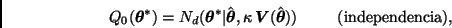
¿Qué es el método Monte Carlo?
El método de Montecarlo es un método no determinativo o estadístico numérico, usado para aproximar expresiones matemáticas complejas y costosas de evaluar con exactitud.El método se llamó así en referencia al Casino de Monte Carlo (Principado de Mónaco) por ser “la capital del juego de azar”, al ser la ruleta un generador simple de números aleatorios. El nombre y el desarrollo sistemático de los métodos de Monte Carlo datan aproximadamente de 1944 y se mejoraron enormemente con el desarrollo de la computadora.
(http://es.wikipedia.org/wiki/M%C3%A9todo_de_Montecarlo)
¿Cual es su origen?
¿Cual es su origen?
La invención del método de Monte Carlo se asigna a Stanislaw Ulam y a John von Neumann. Ulam ha explicado cómo se le ocurrió la idea mientras jugaba un solitario durante una enfermedad en 1946. Advirtió que resulta mucho más simple tener una idea del resultado general del solitario haciendo pruebas múltiples con las cartas y contando las proporciones de los resultados que computar todas las posibilidades de combinación formalmente. Se le ocurrió que esta misma observación debía aplicarse a su trabajo de Los Álamos sobre difusión de neutrones, para la cual resulta prácticamente imposible solucionar las ecuaciones íntegro-diferenciales que gobiernan la dispersión, la absorción y la fisión.
Técnicas de validación estadística
En cualquier trabajo de modelado y muy especialmente en simulación, el proceso de plantear hipótesis, construir el modelo y validarlo es un proceso cíclico. Muchas veces las partes individuales de un modelo parecen representar la realidad, pero cuando se consideran en conjunto, resulta en un pobre reflejo de la conducta del sistema en general.
Existen dos formas de validar un modelo:
a) Permitir que el usuario chequee que la simulación se desarrolla como debe. El usuario no tiene por qué entender el código, pero sí debe poder entender el diagrama de actividades y debe participar activamente en el planteo de los objetivos del trabajo y por ende en la lógica y detalles de la simulación. Es importante brindarle resultados visuales del comportamiento de las colas, entidades y el uso de recursos, que le permitan ver si la simulación se comporta en forma similar al sistema real.
b) Brindar estadísticas que confirmen que la simulación produce resultados similares a los del sistema real. Esto necesita de una recolección de datos adicional acerca de promedios de largos de colas, tiempo de ocupación de los servidores y tiempos de espera, los que se confrontarán con los obtenidos mediante la simulación.
Cadenas de Markov
Una cadena de markov consta de unos estados E1 E2 E3 E4…..En. que inicialmente en un tiempo 0 o paso 0 se le llama estado inicial, además de esto consta de una matriz de transición que significa la posibilidad de que se cambie de estado en un próximo tiempo o paso.
Una matriz de transición para una cadena de Markov de n estado es una matriz de n X n con todos los registros no negativos y con la propiedad adicional de que la suma de los registros de cada columna (o fila) es 1. Por ejemplo: las siguientes son matrices de transición.
Ejemplo:
En un país como Colombia existen 3 operadores principales de telefonía móvil como lo son tigo, Comcel y movistar (estados).
Los porcentajes actuales que tiene cada operador en el mercado actual son para tigo 0.4 para Comcel 0.25 y para movistar 0.35. (estado inicial)
Se tiene la siguiente información un usuario actualmente de tigo tiene una probabilidad de permanecer en tigo de 0.60, de pasar a Comcel 0.2 y de pasarse a movistar de 0.2; si en la actualidad el usuario es cliente de Comcel tiene una probabilidad de mantenerse en Comcel del 0.5 de que esta persona se cambie a tigo 0.3 y que se pase a movistar de 0.2; si el usuario es cliente en la actualidad de movistar la probabilidad que permanezca en movistar es de 0.4 de que se cambie a tigo de 0.3 y a Comcel de 0.3. Partiendo de esta información podemos elaborar la matriz de transición.
La suma de las probabilidades de cada estado en este caso operador deben ser iguales a 1
Po= (0.4 0.25 0.35) → estado inicial
También se puede mostrar la transición por un método grafico
Ahora procedemos a encontrar los estados en los siguientes pasos o tiempos, esto se realiza multiplicando la matriz de transición por el estado inicial y asi sucesivamente pero multiplicando por el estado inmediatamente anterior.
Como podemos ver la variación en el periodo 4 al 5 es muy mínima casi insignificante podemos decir que ya se a llegado al vector o estado estable.
(http://investigaciondeoperaciones2markov.blogspot.com/p/teoria-y-ejemplos.html)
(http://investigaciondeoperaciones2markov.blogspot.com/p/teoria-y-ejemplos.html)
Algoritmos de Metrópolis-Hastings
Este algoritmo construye una cadena de Markov apropiada definiendo las probabilidades de transición de la siguiente manera.
Sea 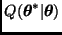 una distribución de transición (arbitraria) y definamos
una distribución de transición (arbitraria) y definamos
Algoritmo. Dado un valor inicial 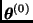 , la
, la 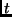 -ésima iteración consiste en:
-ésima iteración consiste en:
1. generar una observación 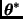 de
de 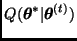 ;
;
2. generar una variable 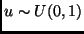 ;
;
3. si 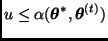 , hacer
, hacer 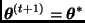 ; en caso contrario, hacer
; en caso contrario, hacer 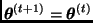 .
.
Este procedimiento genera una cadena de Markov con distribución de transición
La probabilidad de aceptación 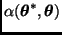 sólo depende de
sólo depende de 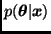 a través de un cociente, por lo que la constante de normalización no es necesaria.
a través de un cociente, por lo que la constante de normalización no es necesaria.
Comentario. La versión original del algoritmo de Metropolis toma 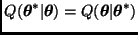 , en cuyo caso
, en cuyo caso
Dos casos particulares utilizados comúnmente en la práctica son:
con 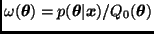 .
.
En la práctica es común utilizar, después de una reparametrización apropiada, distribuciones de transición normales ó 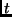 de Student ligeramente sobredispersas, e.g.
de Student ligeramente sobredispersas, e.g.
ó
donde 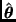 y
y 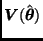 denotan a la media y a la matriz de varianzas-covarianzas de la aproximación normal asintótica para
denotan a la media y a la matriz de varianzas-covarianzas de la aproximación normal asintótica para 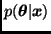 , respectivamente, y
, respectivamente, y 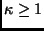 es un factor de sobredispersión.
es un factor de sobredispersión.
Muestreo de GIBBS
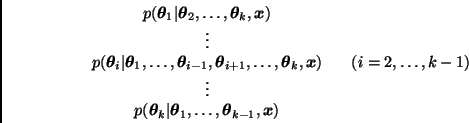
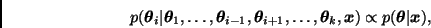
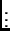
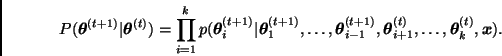

Al igual que el algoritmo de Metropolis, el algoritmo de Gibbs permite simular una cadena de Markov 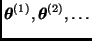 con distribución de equilibrio
con distribución de equilibrio 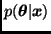 . En este caso, sin embargo, cada nuevo valor de la cadena se obtiene a través de un proceso iterativo que sólo requiere generar muestras de distribuciones cuya dimensión es menor que
. En este caso, sin embargo, cada nuevo valor de la cadena se obtiene a través de un proceso iterativo que sólo requiere generar muestras de distribuciones cuya dimensión es menor que 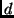 y que en la mayoría de los casos tienen una forma más sencilla que la de
y que en la mayoría de los casos tienen una forma más sencilla que la de 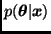 .
.
Sea 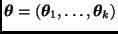 una partición del vector
una partición del vector 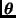 , donde
, donde 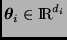 y
y 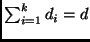 . Las densidades
. Las densidades
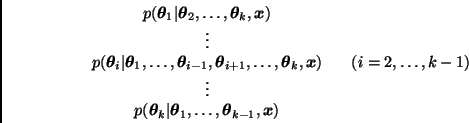
se conocen como densidades condicionales completas y en general pueden identificarse fácilmente al inspeccionar la forma de la distribución final 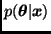 . De hecho, para cada
. De hecho, para cada 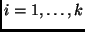 ,
,
donde 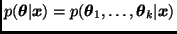 es vista sólo como función de
es vista sólo como función de 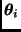 .
.
Dado un valor inicial 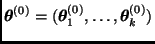 , el algoritmo de Gibbs simula una cadena de Markov en la que
, el algoritmo de Gibbs simula una cadena de Markov en la que 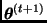 se obtiene a partir de
se obtiene a partir de 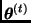 de la siguiente manera:
de la siguiente manera:
generar una observación 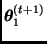 de
de 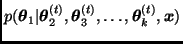 ;
;
generar una observación 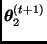 de
de 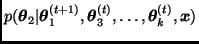 ;
;
generar una observación 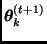 de
de 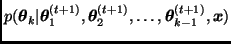 .
.
La sucesión 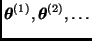 así obtenida es entonces una realización de una cadena de Markov cuya distribución de transición está dada por
así obtenida es entonces una realización de una cadena de Markov cuya distribución de transición está dada por
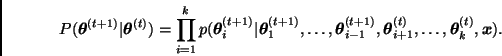
Comentario. En ocasiones la distribución final implica cierta estructura de independencia condicional entre algunos de los elementos del vector 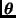 . Es estos casos es común que muchas de las densidades condicionales completas se simplifiquen.
. Es estos casos es común que muchas de las densidades condicionales completas se simplifiquen.

Algoritmo Templado Simulado
Algoritmo de Wang-Landau
Simulated annealing (SA) o recocido simulado es un algoritmo de búsqueda meta-heurística para problemas de optimización global; el objetivo general de este tipo de algoritmos es encontrar una buena aproximación al valor óptimo de una función en un espacio de búsqueda grande. A este valor óptimo se lo denomina"óptimo global".
El método fue descrito independientemente por Scott Kirkpatrick, C. Daniel Gelatt y Mario P. Vecchi en 1983 y por Vlado Černý en 1985. El método es una adaptación del algoritmo Metropolis-Hastings, unmétodo deMontecarloutilizado para generar muestras de estados de unsistema termodinámico.
ALGORITMO DE TEMPLADO SIMULADO
El algoritmo Wang-Landau es una extensión del método de Monte Carlo, propuesto por Fugao Wang y David P. Landau, que permite calcular la densidad de estados de un sistema dado sin tener ningún conocimiento previo sobre ella. Se dice entonces que la densidad de estados se calcula on the fly, o sea durante la simulación. El algoritmo es independiente de la temperatura (un problema común con otros algoritmos Monte Carlo) y es fácil de implementar.
Este algoritmo fue pensado inicialmente para muestrear el espacio de configuraciones de ciertos sistemas que no podían ser tratados mediante el algoritmo de Metropolis. El algoritmo de Metropolis realiza un muestreo usando el factor de Boltzmann para aceptar o descartar configuraciones. Metropolis funciona bien si todas las configuraciones posibles del sistema se encuentran dentro de un rango relativamente angosto de energías.
Suscribirse a:
Entradas (Atom)